Resistors are an essential component and can be found in almost every electrical and electronic circuit (if not all).
A resistor can provide many functions in a circuit, but its main purpose is to limit current.
However, when it comes to limiting current, power is dissipated in the form of heat.
But, which resistor dissipates more power? The amount of power that a resistor comes down to a lot of factors, but a smaller resistor will dissipate more power due to the fact that it has a lower surface area and a higher current flowing through it.
In saying that, there are other considerations to take into account which comes down to Ohm’s Law, material the resistor is made of, and surface area of the resistor.
I will cover these below.
Why do resistors dissipate power
To begin with, let us understand why resistors actually dissipate power.
Without getting into too much detail, you might be aware of the first Law of thermodynamics, also known as the Law of Conservation of energy which states that energy can neither be created or destroyed.
It can either be transferred or changed from one form to another.
For example, the sun transforms nuclear energy into heat and light.
When current flows through a resistor, slowing or limiting it causes a transfer of energy. The energy transfer in this instance is from kinetic (vibration of atoms or charge), to heat.
The slowing of molecules largely depends on the material that the resistor is made of which tends to be a conductor (as current needs to flow through it as well)
All conductors have some form of ‘resistance’.
Therefore, the resistor dissipates power in the form of heat.
What determines which resistor dissipates more power?
Now that we know why a resistor dissipates power, we can look at what factors determine which of the resistors will dissipate the most power.
The first major factor that will determine how much power a resistor will dissipate comes down to Ohm’s law.
Ohm’s law is a law that states that the current through a conductor (between two points), is proportional to the voltage between those two points. It can be seen in the formula shown below.
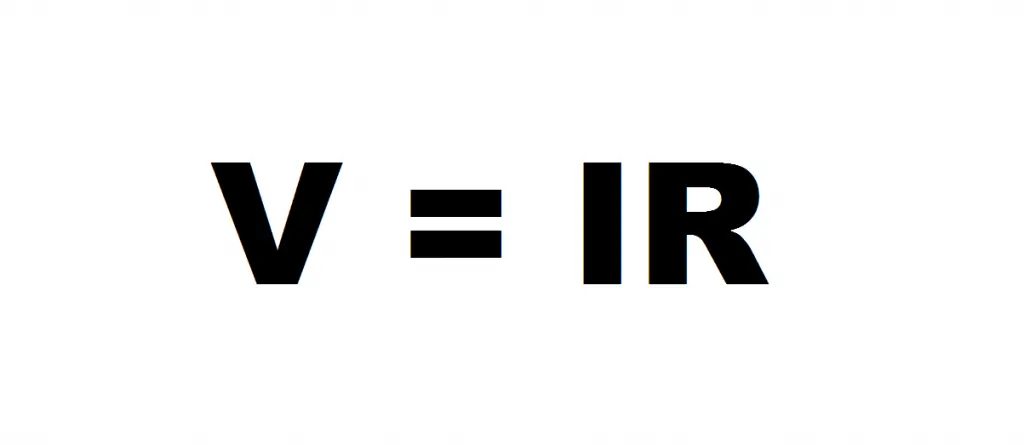
This fundamental formula is used when designing and diagnosing circuits.
It lets you calculate voltage, current , and resistance of a circuit or at a specific component in a circuit.
Another formula that is important to us in determining how much power is dissipated by a resistor is shown below.
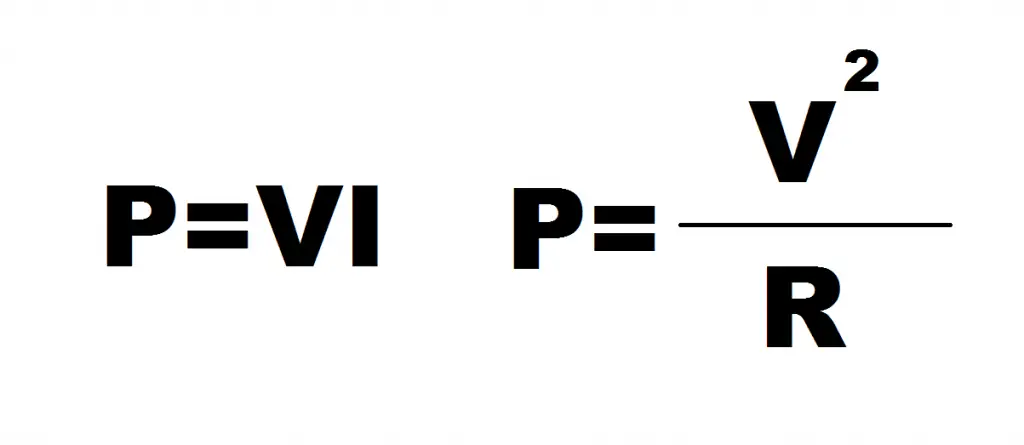
There are many ways to calculate power dissipation, but these are the two most common using voltage, current and resistance.
Next, let’s take a look at how you would go about calculating how much power a resistor dissipates using these formulas which will give an indication of which type of resistor dissipates more power.
How do you calculate how much power a resistor dissipates
Let’s take a look at an example of how to calculate how much power a resistor dissipates in a simple circuit.
Below is a simple circuit with a voltage source, and resistor.

The good news is that knowing how to calculate power dissipation in this simple type of circuit will apply to every circuit no matter its complexity.
So, we will go about finding how much power the resistor in this circuit dissipates using the two formulas we saw earlier which are; V= IR and P = V2/R.
Below are the list of steps required to find the power dissipation of the resistor R1 in the circuit above:
- Find the total current in the circuit
- Find the voltage across the resistor using the current value (since this is a series circuit, the current is the same throughout the whole circuit)
- After the voltage is found across the resistor, use that voltage and value of resistor R1 to find the Power dissipated by the resistor.
STEP 1:
First we need to find the total current in the circuit. This requires us to use the V=IR equation.
Since we know the values of V and R, we can rearrange the formula to make I the subject which gives us the following formula I = V/R1.
So plugging the values into the formula I = 5 /10, gives us a current of 0.5 amps.
STEP 2:
Now that we have the total current in the circuit (since this is a series circuit where current is the same throughout the circuit), we can calculate the voltage across the resistor.
We will go back to using the formula of V = IR.
In this instance, the value of R in the formula would be the value of the resistor we are trying to find the voltage across which is 10 ohms in this example.
So, using the current we just calculated, and the value of resistor R1 in the formula, V = 0.5 x 10, we get a voltage value of 5 volts.
This tells us that there is voltage drop of 5 volts across resistor R1.
STEP 3:
The last and final step requires us to use the formula P = V2 / R.
V in this equation is the voltage drop value across resistor R1(5 volts), and R is the value of R1 (10 ohms).
Plugging these values in the equation P = 52 / 10, gives us a P value of 2.5 watts.
This is the value of how much power the resistor dissipates in the circuit in question.
Why a smaller resistor dissipates more power
From the example above we saw that a 10 ohm resistor dissipates 2.5 watts of power.
What if we decrease the value of the resistor from 10 to 5 ohms while keeping the voltage value the same?
What happens to the amount of power dissipated across the resistor?
The value of power now increases from 2.5 watts to 5 watts.
This is due to the inversely proportional relationship between R and P in the P = V2 / R equation.
An increase in R will see a decrease in P, and a decrease in R will result in an increase in P.
Also, another reason a smaller resistor will dissipate more power comes down to its surface area.
A smaller, or lower value resistor has a lower penetration of the magnetic field which leads to an increase in current flow within a smaller surface area.
Due to this there is greater power dissipation in the form of heat loss.
Do bigger resistors dissipate more power that smaller resistors?
As we saw with the examples above, a smaller resistor will dissipate more power due to Ohm’s law, as well as its physical dimensions.
But, why are bigger resistors used for higher power applications? Does that mean that they dissipate more power?
The main reason a bigger resistor is used in higher power applications is because of its ability to handle those high levels of power.
This comes down to its size and material. They are specifically designed for high power applications.
A bigger resistor unlike a small resistor, has a larger surface area giving it the ability to dissipate heat and therefore power better.
This is why you would use a larger resistor in high power applications because they can dissipate that power more efficiently.
Do all resistors dissipate the same amount of power?
The simple answer is no.
All resistors dissipate different amounts of power.
As you from earlier, this comes down to the resistance value which is influenced largely by what material it is made of, as well as its size.
All resistors have their own power rating, which is labelled on the resistor’s packaging, the specification section online or on its datasheet.
Power rating of a resistor
So, every resistor dissipates different amounts of power.
Lucky for us, this value is given to us.
It is known as the resistor’s Power Rating or Wattage Rating.
Every resistor has a maximum power rating which is governed by its physical size. The greater the surface area, the better its ability to dissipate power in the form of heat.
This rating is defined for ambient temperatures of 70 degrees celsius (158 degrees fahrenheit) and above.
Exceeding the maximum power rating of the resistor will cause it to be damaged.
While resistors have colour coding that indicate its resistance value and tolerance, this colour coding does not indicate the power rating of the resistor.
You will find the power rating on the packaging that the resistor comes packed in. Or, when buying them online, the specifications section of the resistor should indicate the power rating.
Does a resistor dissipate more power in series or parallel?
You might be aware that there are two types of circuit configurations that a resistor can be used in; Series or Parallel (or a combination of both).
In a Series configuration, the current is constant throughout the circuit, whereas in a parallel configuration, the voltage is constant.
So, does a resistor dissipate more power in series or parallel?
The configuration a resistor is subject to does not matter when it comes to power dissipation.
It comes down to the voltage and current that the resistor is subject to in either configuration.
The great news is that Ohm’s law and the power formula can be used in both configurations to calculate the power that the resistor will dissipate and then you can go about choosing a resistor with the right power rating accordingly.
Does the material that the resistor is made of affect how much power it dissipates?
The material is one of the factors that determines how much power a resistor will dissipate.
There are three typical types of resistors ; Wirewound, Metal Film, and Carbon.
Wirewound resistors are used for larger power resistors with higher power ratings, whereas Metal film and Carbon resistors are used for lower power applications.
No matter what type of material, Ohm’s law still applies when it comes to calculating power dissipation.
Below is a table of the different types of materials used and their typical power ratings.
| Material | Power Rating |
| Metal Film | Less than 3 watts |
| Carbon | Less than 5 watts |
| Wirewound | Up to 500 watts |
The importance of checking how much power a resistor dissipates?
Every resistor has a maximum power rating for a reason. Exceeding this value will cause the resistor to be damaged.
This can lead to other problems in the circuit.
Also, it will set you back on time and money.
Calculating how much power the resistor will be subject to, and picking a resistor with the right maximum power rating, will save you a lot of stress in the long run.